Ragu for Orchard: Recursion Al Dente

This blog post is intended for a technical audience. Reader discretion is advised.

Project Tachyon, as I introduced in my last blog post, leans heavily on proof-carrying data (PCD) to tackle the toughest challenges in scaling Zcash’s shielded payments. We need a toolkit aimed specifically at the cryptography we deployed in our Orchard payment protocol — recursive proofs with the Pasta curve cycle — that can accomodate our specific needs and adapt to the active landscape of new PCD protocols based on accumulation (or “folding”) schemes.

We have several specific needs, including:

• We need a solution adapted for Orchard. If we use something off-the-shelf like kimchi — which is certainly an option to consider — we'll be forced to use cryptography that is years out of date by now and comparatively inefficient for our protocol.¹ We need our proving system to meet the needs of Orchard (and Tachyon), not the other way around.²
• We need something simpler to write circuits for. We don't mind writing circuits by hand, but when the underlying arithmetization forces us to make intense optimization efforts like we did with the halo2_proofs and orchard crates, the resulting codebase is extremely difficult to understand and maintain, not to mention audit.³ My ideal choice would be to use an R1CS-like arithmetization with escape hatches for more advanced stuff (e.g. lookups) in the situations where it's necessary.⁴
• We need to handle non-uniform circuits efficiently. Our PCD tree will handle many different circuits at different nodes, and when the underlying protocol natively supports switching between these (according to well-defined rules) it is far simpler and more efficient than an ad hoc approach with pre-processed proving keys that have to be carried around through the computational graph.

I've been working on a PCD toolkit called ragu, written in Rust, that is intended to fit within Zcash's performance and complexity budget. It supports non-uniform circuits, uses a simple R1CS-like arithmetization, avoids complicated subprotocols, avoids FFTs most of the time, supports split accumulation, and is built specifically for the Pasta curves that are native to the Orchard shielded protocol. It's still under heavy development and the underlying proving system is not a main focus of my development effort; my current priority is building the API that I want for Tachyon, and working backwards from there to find the cryptography that meets our needs.

Currently, ragu uses an arithmetization similar to R1CS and its API is inspired heavily by what you'd see in other Rust toolkits like arkworks, kimchi and our very own bellman used in Sapling. Thanks to numerous language features that have shipped in Rust in the last several years, we can really improve on those APIs and make our circuit synthesis code much more efficient, which is absolutely necessary for various things like non-uniform circuits.

I'm not ready to share the code yet, but I am excited to share some of the details about the crate's design decisions so far.

🔗Speedy Circuit Synthesis

In most SNARK toolkits the witness generation logic is embedded alongside the codepaths that are responsible for constructing the corresponding constraints, allowing common abstractions to be shared and reducing the chance of fatal soundness bugs. This gets tricky when the circuit must be synthesized in a context where the witness is unknown, like during the one-time parameter generation of most pre-processing SNARKs, since the code must accomodate both contexts simultaneously with as little overhead as possible.

However, because our protocol leverages non-uniform circuits (as in HyperNova and similar schemes) and does not have a pre-processing step, the circuit synthesis code is frequently invoked⁵ throughout the PCD tree in order to transition from one circuit to another. It is also applied during the decision procedure by the verifier. This means that circuit synthesis is a hot path that must be optimized.

🔗Maybe<T>

The first optimization and ergonomic improvement in ragu comes from the use of an abstract alternative to Option<T> for encoding witness values. In most Rust-based SNARK toolkits the circuits are written so that (auxillary) witness information might exist at runtime and is therefore represented with Option<T>. During proof generation the witness information is transformed into a fallible Result<T, SynthesisError> (or similar) and the error case is propagated upward and caught by the driver of the synthesis if needed. This works, with several drawbacks:

1. The Option<T> exists throughout synthesis in contexts where we can theoretically know (statically) that it should exclusively occupy the Some(T) variant or only the None variant, depending on the underlying driver of synthesis. After monomorphization, we can know with certainty that an Option<T> is not actually required, but the compiler cannot optimize it away! This leads to pointless branching at runtime, wasted stack space for storing discriminants and completely unnecessary (and potentially large) allocations outside of proof generation.
2. The failure case of an unexpected missing witness needs to be handled: either we panic! at runtime (a bad idea here!) or we could bubble it up as an error to the driver. This requires every code path that potentially touches witness data to propagate an error, even though only very few codepaths actually result in any error during synthesis.⁶ Once you start dealing with iterators, multi-threaded synthesis optimizations, embedded witness generation logic, etc. it gets obnoxious to write code full of pointless error handling cases that should be prevented at compile-time.
3. It's best to avoid leveraging Option<T>'s monadic operators outside of limited areas of the API, since it will require the compiler to codegen these operations even in contexts where they're never invoked; the compiler cannot optimize any of this away in dead-code elimination passes because it's using a runtime enum discriminant to conditionally invoke functions. This is unfortunate because it's very convenient to invoke these operators on infallible morphisms.

The ragu crate introduces a higher-kinded abstraction called Maybe<T> which is a generalization of an Option<T> except that it's a kind of “indexed” monad: the concrete type of a Maybe<T> is either represented by an Always(T) type that transparently wraps T or a zero-sized Empty type that mimics (). In other words, it is an opaque generalization over the variant of an Option rather than the type.

The trait looks something like this, from a user's perspective:

pub trait MaybeKind {
    type Rebind<T>: Maybe<T, Kind = Self>;
}

pub trait Maybe<T> {
    type Kind: MaybeKind;

    fn just<R>(f: impl FnOnce() -> R) -> <Self::Kind as MaybeKind>::Rebind<R>;
    fn with<R>(
        f: impl FnOnce() -> Result<R, super::Error>,
    ) -> Result<<Self::Kind as MaybeKind>::Rebind<R>, super::Error>;
    fn take(self) -> T;
    fn map<U, F>(self, f: F) -> <Self::Kind as MaybeKind>::Rebind<U>
    where
        F: FnOnce(T) -> U;
    fn view(&self) -> <Self::Kind as MaybeKind>::Rebind<&T>;
    fn snag(&self) -> &T {
        self.view().take()
    }
    
    /* ... and many omitted methods ... */
}

The full API is a limited form of the Option<T> API with some methods that I'll highlight:

• Maybe<T>::just can be used to create a Maybe<T> using the provided closure if the backing store is Always, and ignoring the provided closure if it's Empty. In the Empty case not only is the closure not called but it cannot survive dead code elimination and the resulting Empty is zero-sized, consuming no memory.
• Maybe<T>::with is similar to Maybe<T>::just except it propagates any failure that might emerge in the provided closure, which can happen during circuit synthesis for reasons other than a missing witness.
• Maybe<T>::take can be used to obtain the content within, which is a simple no-op move if the backing store is Always(T), but if the backing store is Empty then this fails at compile-time. You should only call take in contexts where the API guarantees the backing store is Always(T) as I'll discuss later.
• Maybe<T>::map (and its friends like and_then) work like you'd expect. If the backing store is Empty they are no-ops and their closures also must be eliminated by the compiler, otherwise the operation is always applied and does not accomodate a failure case. There's a little higher-kinded type glue but it's hidden from the user.
• Maybe<T>::view works kind of like Option<T>::as_ref except that as_ref is defined for &T so view avoids the ambiguity.⁷ I also have a view_mut method that comes in handy.
• Maybe<T>::snag is a convenience method that is useful for avoiding moves when necessary.

In order to assist readability and mitigate issues with Rust's type inference rules the underlying generic driver D provides D::with and D::just methods that proxy to the backing Maybe<T>'s methods, but otherwise, everything behaves and looks like you're dealing with an infallible Option<T> type. Witness generation code that might trigger an error looks like this:

let b = D::with(|| {
    let proof = &witness.snag()[i];
    let proof_id = *proof_ids[i].value().snag();
    let y = y.value().take();
    let z = z.value().take();

    let mut tmp = self.multi.rXz(
        z,
        &proof.a,
        &proof.b,
        &proof.c,
    );

    for (tmp, s) in tmp.iter_mut()
                       .zip(self.multi.wXyz(proof_id, y, z)?)
    {
        *tmp += s;
    }

    Ok(tmp)
});

Here, witness, proof_id[i].value(), y and z are all Maybe-types and yet there is no need to handle the runtime possibility of them being absent. This is a zero-cost abstraction. The code looks like it's working directly with the values because that's what it's actually doing at runtime.

There are many other situations where this new abstraction can enable convenient circuit synthesis code. As an example, if you have a Vec<M> where M: Maybe<T> then when the driver doesn't need a witness the value M is a zero-sized type and so Vec<M> never allocates at runtime; otherwise, it's the exact same as a Vec<T>. This also means that you can borrow a Maybe<&[T]> from a &[Maybe<T>] without any overhead or unsafe code.⁸ These things are not possible in existing Rust SNARK toolkits which have to pay for the pointless memory layout consequences at runtime.

🔗Driver

I've alluded to this concept of a “driver” which can be thought of as a compile-time specialized context for how the circuit is synthesized at runtime. The driver acts as a substitute for ConstraintSystem<F> and exposes a more generic interface to the synthesis logic that gives the driver much more flexibility. This is what an abbreviated description of a driver is:

pub trait Driver {
    type F: Field;
    type W: Clone;
    const ONE: Self::W;
    type MaybeKind: maybe::MaybeKind;
    type IO: Sink<Self, Self::W>;
}

pub type Witness<D, T> = <<D as Driver>::MaybeKind as maybe::MaybeKind>::Rebind<T>;

The Driver is defined for a concrete driver that supports a specific field F but the trait itself is not generic over one, unlike ConstraintSystem<F>. This emerges naturally and results in fewer generics scattered around; just use D::F to refer to the field instead of F in cases where the type system hasn't unified it with another type you already know about. (I've written a lot of different gadgets with this API and I can assure you this is much better.)

The D::W associated type represents an abstract wire type. All you can do is clone it. In other Rust SNARK toolkits when you ask the backend to allocate a variable (or wire) in your constraint system it will return a concrete wire type that internally points to a specific part of the witness for later use by the backend. This usually works just fine, but in our case we have drivers with various different needs for what this wire value should actually represent.

• During proof generation: The wire represents a position in the witness just like in other toolkits.
• During verification of a non-succinct witness: The wire represents the value of the witness (a field element) read directly from the proof.
• During the computation of public inputs: As we'll see later, it becomes far simpler if the circuit code can reconstruct the public inputs (as the circuit intends to interpret them) if the circuit code that constructs the public input during verification is the same as the code that does so within the circuit itself. In this case, the wire value is also just a value because we only care about the public input values and none of the interstitial values used to compute it.

However, the most important benefit of this abstraction is for dealing with evaluation of non-uniform circuit polynomials.⁹ Briefly, ragu internally uses a 4-variate polynomial to describe all of the circuits in the PCD tree.

🔗

We do not store this entire polynomial in memory because it would be absolutely humongous. We only ever need to evaluate a restricted form of this polynomial (with zero or one free variables) so it's easier, simpler and more efficient to evaluate the polynomial as part of circuit synthesis itself.

• During verification: Computation of uses a driver that feeds the partially evaluated polynomial into the circuit as the abstract wire value. The circuit synthesis code is inadvertently evaluating the polynomial on behalf of the backend! This is fantastic because it doesn't require any extra heap allocation to compute. (The remaining restrictions are simple because the polynomials are either succinct or of low degree.)
• During proof generation: Computations of , have their own distinct drivers that efficiently evaluate the polynomials in their own way, using similar techniques to get the circuit synthesis code to evaluate the polynomials partially on our behalf.

Finally, there are three additional methods that the Driver provides:

    fn mul(
        &mut self,
        values: impl FnOnce() -> Result<(Self::F, Self::F, Self::F), SynthesisError>,
    ) -> Result<(Self::W, Self::W, Self::W), SynthesisError>;

    fn add<L: IntoIterator<Item = (Self::W, Self::F)>>(
        &mut self,
        lc: impl FnOnce() -> L,
    ) -> Result<Self::W, SynthesisError>;

    fn enforce_zero<L: IntoIterator<Item = (Self::W, Self::F)>>(
        &mut self,
        lc: impl FnOnce() -> L,
    ) -> Result<(), SynthesisError>;

The mul method produces a multiplication constraint given a closure that returns an assignment for the two input wires and one output wire of a multiplication gate in an arithmetic circuit. The closure is only invoked when a witness is expected, so inside the closure you can call Maybe<T>::take() just as you can do in the with method. The method returns three new wires that can be used in linear constraints.

The add and enforce_zero methods, in contrast, only invoke their closure when we do not expect a witness. The add method effectively takes a linear combination of wires and computes a new wire — in the underlying proving system, this just produces a virtual wire that costs (essentially) nothing and sometimes improves synthesis performance. The enforce_zero method creates a linear constraint that requires some linear combination of previously-allocated wires to be zero.

🔗Circuit

The Circuit<F> trait that you're more familiar with if you've used halo2 or bellman essentially consists of a single method called synthesize that creates all of the constraints and the witness data (if applicable) given a ConstraintSystem<F>. The ragu crate uses a much more generalized dataflow to deal with edge cases that this API design cannot easily handle. The circuit consists of three methods: input, main and output which work as follows:

🔗

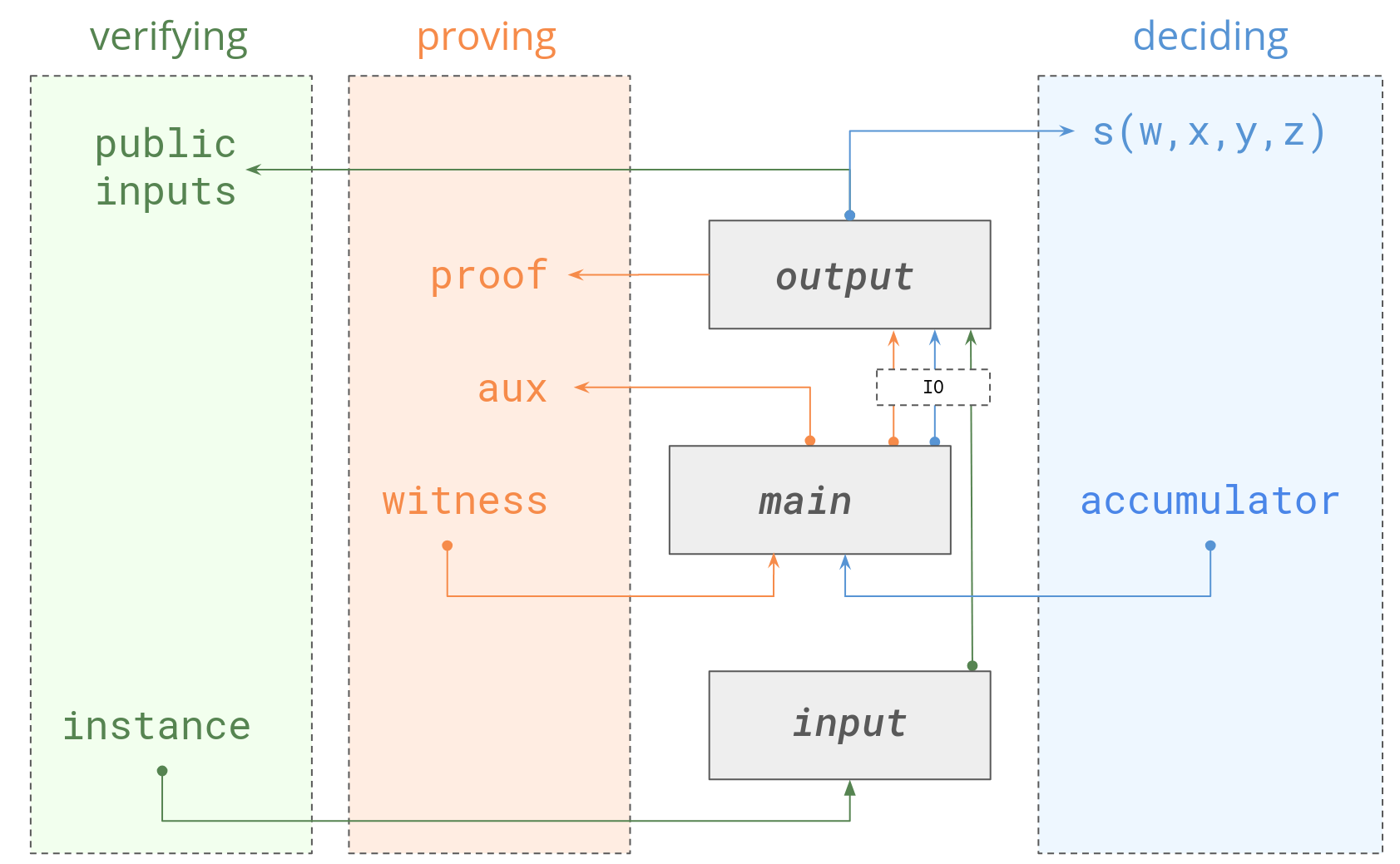
This arrangement splits out some of the logic that took place solely in the old synthesize method. As you can see from the diagram, the verification path through the circuit code starts from a circuit-defined instance type that is fed into the input method, and rather than used by the main method is directly fed into the output method to obtain the public input. In proving, the path starts as a witness that goes through the main method and takes the same route through the output method to synthesize the same public inputs, ensuring the same logic that is used to generate and relate public inputs between the circuit and outside code reuses the same code paths and abstractions.

There are further advantages to this more complicated arrangement. The core proving code (in main) can produce auxillary data in the process which is used by the user who invoked the proof generator; this is useful when the witness generation procedure is itself performing “folding” operations and constructing accumulators that will be needed to verify the proof. And circuits with simple behaviors can plumb these procedures together. As an example, if you have a circuit where the instance itself is identical to the witness, the main procedure can invoke the input method and the resulting IO value can be returned from the main method after the remainder of the circuit has been synthesized.

Here's the Circuit trait in all its glory:

pub trait Circuit<F: Field>: Sized {
    type Instance<'instance>;
    type IO<'source, D: Driver<F = F>>;
    type Witness<'witness>;
    type Aux<'witness>;

    fn input<'instance, D: Driver<F = F>>(
        &self,
        dr: &mut D,
        input: Witness<D, Self::Instance<'instance>>,
    ) -> Result<Self::IO<'instance, D>, Error>;

    fn main<'witness, D: Driver<F = F>>(
        &self,
        dr: &mut D,
        witness: Witness<D, Self::Witness<'witness>>,
    ) -> Result<(Self::IO<'witness, D>, Witness<D, Self::Aux<'witness>>), Error>;

    fn output<'source, D: Driver<F = F>>(
        &self,
        dr: &mut D,
        io: Self::IO<'source, D>,
        output: &mut D::IO,
    ) -> Result<(), Error>;
}

🔗Continued...

In the next blog post about ragu I'll be talking about the specific tools and techniques it provides to circuits that will be useful in the development of Tachyon.

One of the things I'll be talking about, as I delve deeper into the underlying proof system that ragu provides, is how the new circuit design facilitates a compositional strategy that drivers can exploit to more efficiently evaluate many polynomial restrictions simultaneously. Because most nodes in the PCD tree share similar behaviors and logic, and because of the nature of our arithmetization, we can use compositional tricks (leveraging the Aux concept, among other things) to build complicated circuits from subcircuits that our proof generation and decision drivers can easily take advantage of to speed up polynomial evaluations considerably.

That's it for now. As always, if you're interested in this kind of work, please get in touch with me!

---